2.4 Limits and Continuity
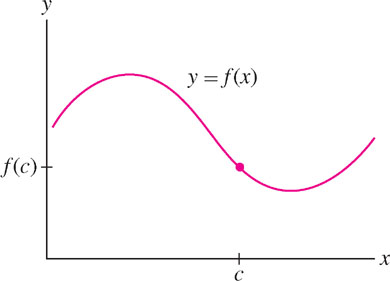
In everyday speech, the word “continuous” intuitively means having no breaks or interruptions. In calculus, continuity is used to describe functions whose graphs have no breaks. If we imagine the graph of a function \(f\) as a wavy metal wire, then \(f\) is continuous if its graph consists of a single piece of wire as in Figure 2.18. A break in the wire as in Figure 2.19 is called a discontinuity.
Now observe in Figure 2.19 that the break in the graph occurs because the left- and right-hand limits as \(x\) approaches \(c\) are not equal and thus \(\lim\limits_{x\rightarrow c} f(x)\) does not exist. By contrast, in Figure 2.18, \(\lim\limits_{x\rightarrow c}f(x)\) exists and is equal to the function value \(f(c)\). This suggests the following definition of continuity in terms of limits.
DEFINITION Continuity at a Point
Assume that \(f(x)\) is defined on an open interval containing \(x=c\). Then \(f\) is continuous at \(x=c\) if\[\lim\limits_{x\rightarrow c}f(x)=f(c)\]If the limit does not exist, or if it exists but is not equal to \(f(c)\), we say that \(f\) has a discontinuity (or is discontinuous)at \(x=c\).
A function \(f(x)\) may be continuous at some points and discontinuous at others. If \(f(x)\) is continuous at all points in an interval \(I\), then \(f(x)\) is said to be continuous on \(I\). If \(I\) is an interval \([a,b]\) or \([a,b)\) that includes \(a\) as a left endpoint, we require that \(\lim\limits_{x\rightarrow a^+} f(x) = f(a)\). Similarly, we require that \(\lim\limits_{x\rightarrow b^-} f(x) = f(b)\) if \(I\) includes \(b\) as a right endpoint. If \(f(x)\) is continuous at all points in its domain, then \(f(x)\) is simply called continuous.
EXAMPLE 1
Show that the following functions are continuous:
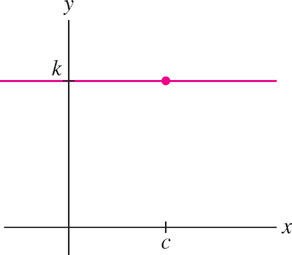
(a) \(f(x)=k\) (\(k\) any constant)
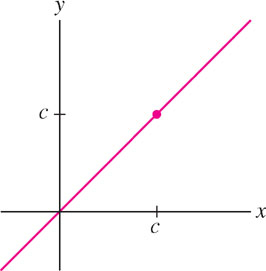
(b) \(g(x)=x^n\) (\(n\) a whole number)
Solution
(a) We have \(\lim\limits_{x\rightarrow c} f(x) = \lim\limits_{x\rightarrow c} k = k\) and \(f(c) = k\). The limit exists and is equal to the function value for all \(c\), so \(f(x)\) is continuous (Figure 2.20).
(b) By Eq. (1) in Section 2.2, \(\lim\limits_{x\rightarrow c} g(x) = \lim\limits_{x\rightarrow c} x^n = c^n\) for all \(c\). Also \(g(c) = c^n\), so again, the limit exists and is equal to the function value. Therefore, \(g(x)\) is continuous. (Figure 2.21 llustrates the case \(n=1\)).
2.4.1 Examples of Discontinuities
To understand continuity better, let’s consider some ways in which a function can fail to be continuous. Keep in mind that continuity at a point \(x=c\) requires more than just the existence of a limit. Three conditions must hold:
- 1. \(f(c)\) is defined.
- 2. \(\lim\limits_{x\rightarrow c}f(x)\) exists.
- 3. They are equal.
63
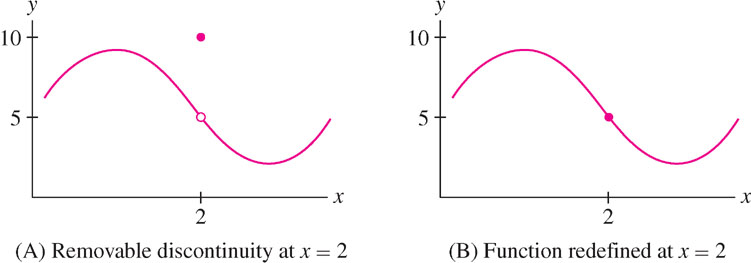
If \(\lim\limits_{x\rightarrow c}f(x)\) exists but is not equal to \(f(c)\), we say that \(f\) has a removable discontinuity at \(x=c\). The function in Figure 2.22(A) has a removable discontinuity at \(c=2\) because\[\underbrace{f(2)=10\quad\text{but}\quad\lim\limits_{x\rightarrow 2}f(x)=5}_{\text{Limit exists but is not equal to the function value}}\]Removable discontinuities are “mild” in the following sense: We can make \(f\) continuous at \(x=c\) by redefining \(f(c)\). In Figure 2.22(B), \(f(2)\) has been redefined as \(f(2) = 5\), and this makes \(f\) continuous at \(x=2\).
A “worse” type of discontinuity is a jump discontinuity, which occurs if the one-sided limits \(\lim\limits_{x\rightarrow c^-}f(x)\) and \(\lim\limits_{x\rightarrow c^+}f(x)\) exist but are not equal. Figure 2.23 shows two functions with jump discontinuities at \(c=2\). Unlike the removable case, we cannot make \(f(x)\) continuous by redefining \(f(c)\).
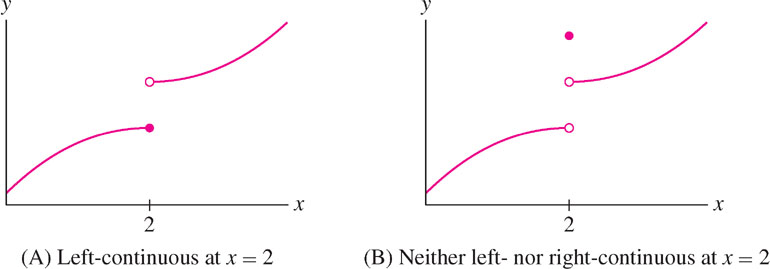
In connection with jump discontinuities, it is convenient to define one-sided continuity.
DEFINITION One-Sided Continuity
A function \(f(x)\) is called:
- Left-continuous at \(x=c\) if \(\lim\limits_{x\rightarrow c^-}f(x) = f(c)\)
- Right-continuous at \(x=c\) if \(\lim\limits_{x\rightarrow c^+}f(x) = f(c)\)
In Figure 2.23 above, the function in (A) is left-continuous but the function in (B) is neither left- nor right-continuous. In the applet below, you can investigate one-sided continuity for this type of function.

The next example explores one-sided continuity using a piecewise-defined function—that is, a function defined by different formulas on different intervals.
EXAMPLE 2 Piecewise-Defined Function
Discuss the continuity of\[F(x) = \left\{ \begin{aligned}x &\quad\text{for } x < 1\\ 3 &\quad\text{for } 1\leq x \leq 3\\ x &\quad\text{for } x > 3 \end{aligned}\right.\]
64
Solution The functions \(f(x) = x\) and \(g(x)=3\) are continuous, so \(F(x)\) is also continuous, except possibly at the transition points \(x=1\) and \(x=3\), where the formula for \(F(x)\) changes (Figure 2.25).
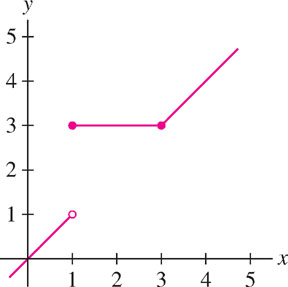
- At \(x=1\), the one-sided limits exist but are not equal: \[\lim\limits_{x\rightarrow 1^-}F(x) = \lim\limits_{x\rightarrow 1^-} x = 1\text{ and } \lim\limits_{x\rightarrow 1^+} F(x) = \lim\limits_{x\rightarrow 1^+} 3 = 3\] Thus \(F(x)\) has a jump discontinuity at \(x=1\). However, the right-hand limit is equal to the function value \(F(1)=3\), so \(F(x)\) is right-continuous at \(x=1\).
- At \(x=3\), the left- and right-hand limits exist and both are equal to \(F(3)\), so \(F(x)\) is continuous at \(x=3\): \[\lim\limits_{x\rightarrow 3^-}F(x) = \lim\limits_{x\rightarrow 3^-} 3 = 3\text{ and } \lim\limits_{x\rightarrow 3^+} F(x) = \lim\limits_{x\rightarrow 3^+} x = 3\]
Question 2.11 Continuity Progress Check 1
Let
\[f(x) = \left\{\begin{aligned} x^2+1 &, x \leq 1 \\ 3-x &, x > 1. \end{aligned}\right.\]
Select the correct statement.
| A. |
| B. |
| C. |
| D. |
We say that \(f(x)\) has an infinite discontinuity at \(x=c\) if one or both of the one-sided limits is infinite (even if \(f(x)\) itself is not defined at \(x=c\)). Figure 2.26 illustrates three types of infinite discontinuities occurring at \(x=2\). Notice that \(x=2\) does not belong to the domain of the function in cases (A) and (B).
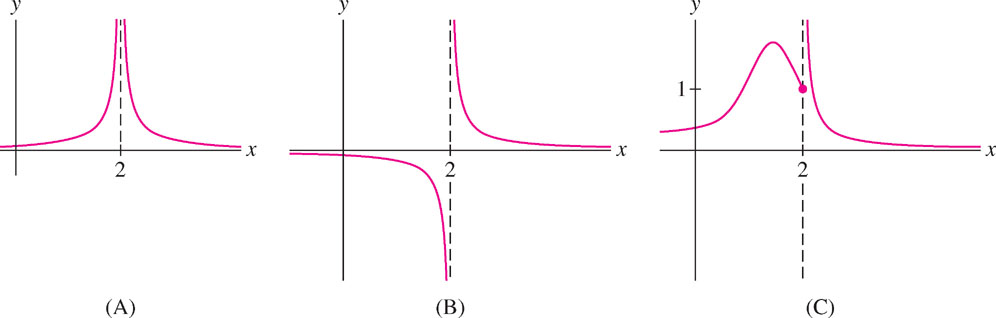
Finally, we note that some functions have more “severe” types of discontinuity than those discussed above. For example, \(f(x) = \sin\tfrac{1}{x}\) oscillates infinitely often between +1 and −1 as \(x\rightarrow 0\) (Figure 2.27). Neither the left- nor the right-hand limit exists at \(x=0\), so this discontinuity is not a jump discontinuity. See Exercises 88 and 89 for even stranger examples. Although of interest from a theoretical point of view, these discontinuities rarely arise in practice.

2.4.2 Building Continuous Functions
Having studied some examples of discontinuities, we focus again on continuous functions. How can we show that a function is continuous? One way is to use the Laws of Continuity, which state, roughly speaking, that a function is continuous if it is built out of functions that are known to be continuous.
THEOREM 1 Basic Laws of Continuity
If \(f(x)\) and \(g(x)\) are continuous at \(x=c\), then the following functions are also continuous at \(x=c\):
- (i) \(f(x)+g(x)\) and \(f(x)-g(x)\)
- (ii) \(kf(x)\)for any constant \(k\)
- (iii) \(f(x)g(x)\)
- (iv) \(\frac{f(x)}{g(x)}\) if \(g(c)\neq 0\)
Proof
These laws follow directly from the corresponding Basic Limit Laws (Theorem 1, Section 2.2). We illustrate by proving the first part of (i) in detail. The remaining laws are proved similarly. By definition, we must show that \(\lim\limits_{x\rightarrow c}(f(x)+g(x)) = f(c) + g(c)\). Because \(f(x)\) and \(g(x)\) are both continuous at \(x=c\), we have
65
\[\lim\limits_{x\rightarrow c} f(x) = f(c) \text{ and } \lim\limits_{x\rightarrow c} g(x)= g(c) \]
The Sum Law for limits yields the desired result:
\[\lim\limits_{x\rightarrow c} (f(x) + g(x)) = \lim\limits_{x\rightarrow c} f(x) + \lim\limits_{x\rightarrow c} g(x) = f(c) + g(c)\]
In Section 2.2, we noted that the Basic Limit Laws for Sums and Products are valid for an arbitrary number of functions. The same is true for continuity; that is, if \(f_1(x),\ldots,f_n(x)\) are continuous, then so are the functions
\[f_1(x)+f_2(x)+\cdots+f_n(x) \text{ and }f_1(x)\cdot f_2(x)\cdots f_n(x)\]
The basic functions are continuous on their domains. Recall (Section 1.3) that the term basic function refers to polynomials, rational functions, \(n^\text{th}\)-root and algebraic functions, trigonometric functions and their inverses, and exponential and logarithmic functions.
When a function \(f(x)\) is defined and continuous for all values of \(x\), we say that \(f(x)\) is continuous on the real line.
THEOREM 2 Continuity of Polynomial and Rational Functions
Let \(P(x)\) and \(Q(x)\) be polynomials. Then:
- \(P(x)\) is continuous on the real line.
- \(\frac{P(x)}{Q(x)}\) is continuous on its domain (at all values \(x=c\) such that \(Q(c)\neq 0\)).
 REMINDER A rational function is a quotient of two polynomials \(\displaystyle \frac{P(x)}{Q(x)}\).
REMINDER A rational function is a quotient of two polynomials \(\displaystyle \frac{P(x)}{Q(x)}\).
Proof
The function \(x^m\) is continuous for all whole numbers \(m\) by Example 1. By Continuity Law (ii), \(ax^m\) is continuous for every constant \(a\). A polynomial
\[P(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0\]
is a sum of continuous functions, so it too is continuous. By Continuity Law (iv), a quotient \(\frac{P(x)}{Q(x)}\) is continuous at \(x=c\), provided that \(Q(c)\neq 0\).
This result shows, for example, that \(f(x) = 3x^4 - 2 x^3 + 8x\) is continuous for all \(x\) and that
\[g(x) = \frac{x+3}{x^2 - 1}\]
is continuous for \(x\neq \pm 1\). Note that if \(n\) is a positive integer, then \(f(x) = x^{-n}\) is continuous for \(x\neq 0\) because \(f(x) = x^{-n} = \frac{1}{x^n}\) is a rational function.
Question 2.12 Continuity Progress Check 2
Is the function \(f(x) = \dfrac{5x-4}{x^2+x+1}\) continuous on the real line?
| A. |
| B. |
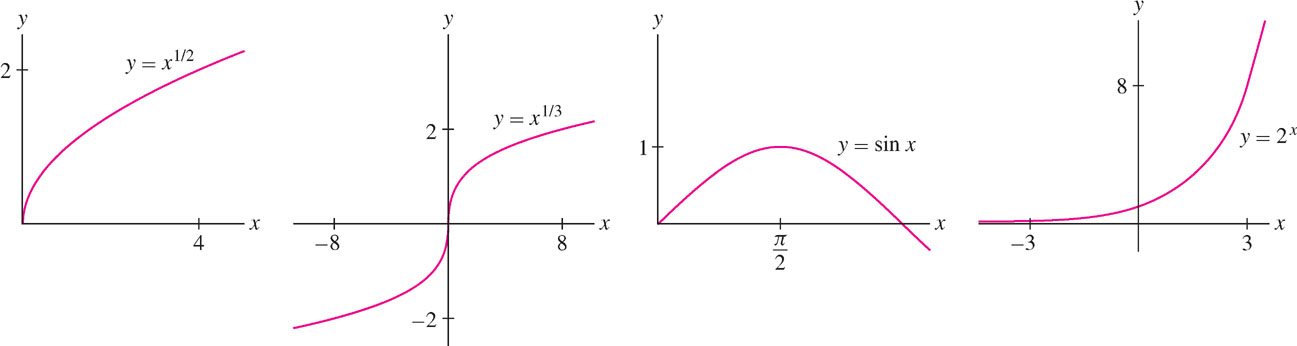
The continuity of the \(n^{\text{th}}\)-root, trigonometric, and exponential functions should not be surprising because their graphs have no visible breaks (Figure 2.28). Similarly, logarithmic functions (introduced in Section 7.2) are continuous. However, complete proofs of continuity are somewhat technical and are omitted.
 REMINDER The domain of \(y = x^{\frac{1}{n}}\) is the real line if \(n\) is odd and the half-line \([0, \infty)\) if \(n\) is even.
REMINDER The domain of \(y = x^{\frac{1}{n}}\) is the real line if \(n\) is odd and the half-line \([0, \infty)\) if \(n\) is even.
THEOREM 3 Continuity of Some Basic Functions
- \(y=x^\frac{1}{n}\) is continuous on its domain for \(n\) a natural number.
- \(y=\sin x\) and \(y=\cos x\) are continuous on the real line.
- \(y=b^x\) is continuous on the real line (for \(b > 0, b\neq 1\)).
- \(y=\log_b x\) is continuous for \(x > 0\) (for \(b > 0, b \neq 1\)).
66
Because \(\sin x\) and \(\cos x\) are continuous, Continuity Law (iv) for Quotients implies that the other standard trigonometric functions are continuous on their domains, consisting of the values of \(x\) where their denominators are nonzero:
\[\tan x =\frac{\sin x}{\cos x}\quad \cot x = \frac{\cos x}{\sin x} \quad \sec x = \frac{1}{\cos x} \quad \csc x = \frac{1}{\sin x}\]
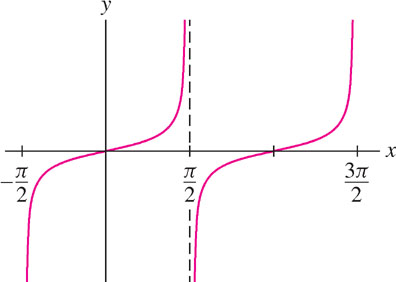
They have infinite discontinuities at points where their denominators are zero. For example, tan x has infinite discontinuities at the points (Figure 2.29)
\[x=\pm\frac{\pi}{2},\pm\frac{3\pi}{2},\pm\frac{5\pi}{2},\cdots\]
Finally, it is important to know that a composition of continuous functions is again continuous. The following theorem is proved in Appendix D.
THEOREM 4 Continuity of Composite Functions
If \(g\) is continuous at \(x=c\), and \(f\) is continuous at \(x=g(c)\), then the composite function \(F(x) = f(g(x))\) is continuous at \(x=c\).
For example, \(F(x) = \left(x^2+9\right)^{\frac{1}{3}}\) is continuous because it is the composite of the continuous functions \(f(x)=x^{\frac{1}{3}}\) and \(g(x)=x^2 + 9\). Similarly, \(F(x) = \cos\left(x^{-1}\right)\) is continuous for all \(x\neq 0\), and \(F(x) = 2^{\sin x}\) is continuous for all \(x\).
More generally, an elementary function is a function that is constructed out of basic functions using the operations of addition, subtraction, multiplication, division, and composition. Since the basic functions are continuous (on their domains), an elementary function is also continuous on its domain by the laws of continuity. An example of an elementary function is
\[F(x) = \sin\left(\frac{x^2+\cos(2^x +9)}{x-8}\right)\]
This function is continuous on its domain \(\{x : x\neq 8\}\).
Question 2.13 Continuity Progress Check 3
Where is \(f(x) = \dfrac{1}{\sqrt{1-\cos x}}\) continuous?
| A. |
| B. |
| C. |
| D. |
2.4.3 Substitution: Evaluating Limits Using Continuity
It is easy to evaluate a limit when the function in question is known to be continuous. In this case, by definition, the limit is equal to the function value:
\[\lim\limits_{x\rightarrow c} f(x) = f(c) \]
We call this the Substitution Method because the limit is evaluated by “plugging in” \(x=c\).
67
EXAMPLE 3
Evaluate (a) \(\lim\limits_{y\rightarrow \frac{\pi}{3}}\sin y\) and (b) \(\lim\limits_{x\rightarrow -1} \dfrac{3^x}{\sqrt{x+5}}\).
Solution
- (a) We can use substitution because \(f(y) = \sin y\) is continuous. \[\lim\limits_{y\rightarrow \frac{\pi}{3}}\sin y = \sin\frac{\pi}{3} = \frac{\sqrt{3}}{2}\]
- (b) The function \(f(x)=\frac{3^x}{\sqrt{x+5}}\) is continuous at \(x=-1\) because the numerator and denominator are both continuous at \(x = −1\) and the denominator \(\sqrt{x+5}\) is nonzero at \(x=-1\). Therefore, we can use substitution: \[\lim\limits_{x\rightarrow -1}\frac{3^x}{\sqrt{x+5}} = \frac{3^{-1}}{\sqrt{-1+5}} = \frac{1}{6}\]
Question 2.14 Continuity Progress Check 4
Evaluate \(\lim\limits_{x\rightarrow -1} \dfrac{\sin(2\pi x)-x^2}{x+2^x}\)
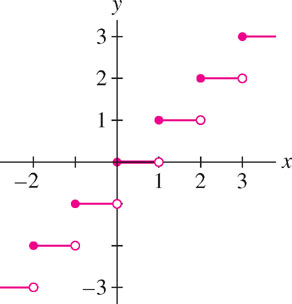
The greatest integer function \([x]\) is the function defined by \([x]=n\), where \(n\) is the unique integer such that \(n\leq x \lt n + 1\) [Figure 2.30]. For example, \([4.7] = 4\).
EXAMPLE 4 Assumptions Matter
Can we evaluate \(\lim\limits_{x \rightarrow 2^-} [x]\) using substitution?
Solution Substitution cannot be applied because \(f(x)\) is not continuous at \(x=2\). Although \(f(2)=2\), \(\lim\limits_{x\rightarrow 2}[x]\) does not exist because the one-sided limits are not equal:
\[\lim\limits_{x\rightarrow 2^+}[x] = 2 \text{ and } \lim\limits_{x\rightarrow 2^-}[x] = 1\]
CONCEPTUAL INSIGHT Real-World Modeling by Continuous Functions
Continuous functions are used often to represent physical quantities such as velocity, temperature, and voltage. This reflects our everyday experience that change in the physical world tends to occur continuously rather than through abrupt transitions. However, mathematical models are at best approximations to reality, and it is important to be aware of their limitations.
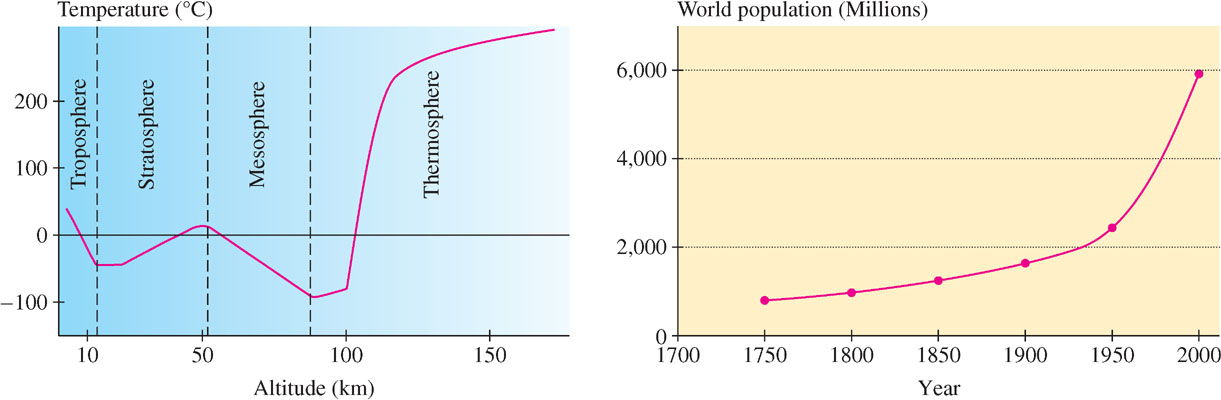
In Figure 2.31, atmospheric temperature is represented as a continuous function of altitude. This is justified for large-scale objects such as the earth’s atmosphere because the reading on a thermometer appears to vary continuously as altitude changes. However, temperature is a measure of the average kinetic energy of molecules. At the microscopic level, it would not be meaningful to treat temperature as a quantity that varies continuously from point to point.
Similarly, the size \(P(t)\) of a population is usually treated as a continuous function of time \(t\). Strictly speaking, \(P(t)\) is a whole number that changes by \(\pm 1\) when an individual is born or dies, so it is not continuous, but if the population is large, the effect of an individual birth or death is small, and it is both reasonable and convenient to treat \(P(t)\) as a continuous function.
68
2.4.4 Summary
- Definition: \(f(x)\) is continuous at \(x=c\) if \(\lim\limits_{x\rightarrow c} f(x) = f(c)\).
- If \(\lim\limits_{x\rightarrow c} f(x)\) does not exist, or if it exists but does not equal \(f(c)\), then \(f\) is discontinuous at \(x=c\).
- If \(f(x)\) is continuous at all points in its domain, \(f\) is simply called continuous.
- Right-continuous at \(x=c\): \(\lim\limits_{x\rightarrow c^+} f(x) = f(c)\).
- Left-continuous at \(x=c\): \(\lim\limits_{x\rightarrow c^-} f(x) = f(c)\).
- Three common types of discontinuities: removable discontinuity [\(\lim\limits_{x\rightarrow c} f(x)\) does not equal \(f(c)\)], jump discontinuity (the one-sided limits both exist but are not equal), and infinite discontinuity (the limit is infinite as \(x\) approaches \(c\) from one or both sides).
- Laws of Continuity: Sums, products, multiples, inverses, and composites of continuous functions are again continuous. The same holds for a quotient \(\frac{f(x)}{g(x)}\) at points where \(g(x)\neq 0\).
- Basic functions: Polynomials, rational functions, \(n^\text{th}\)-root and algebraic functions, trigonometric functions and their inverses, exponential and logarithmic functions. Basic functions are continuous on their domains.
- Substitution Method: If \(f(x)\) is known to be continuous at \(x=c\), then the value of the limit \(\lim\limits_{x\rightarrow c} f(x)\) is \(f(c)\).